Geometria Analitica
La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
Las dos cuestiones fundamentales de la geometría analítica son:
- Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.
- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.
Lo novedoso de la geometría analítica es que representa las figuras geométricas mediante fórmulas del tipo  , donde
, donde  es una función u otro tipo de expresión matemática: las rectas se expresan como ecuacionespolinómicas de grado 1 (por ejemplo,
es una función u otro tipo de expresión matemática: las rectas se expresan como ecuacionespolinómicas de grado 1 (por ejemplo,  ), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia
), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia  , la hipérbola
, la hipérbola 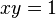 ), etc
), etc
 , donde
, donde  es una función u otro tipo de expresión matemática: las rectas se expresan como ecuacionespolinómicas de grado 1 (por ejemplo,
es una función u otro tipo de expresión matemática: las rectas se expresan como ecuacionespolinómicas de grado 1 (por ejemplo,  ), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia
), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia  , la hipérbola
, la hipérbola 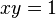 ), etc
), etc
La geometría analítica es la rama de la geometría en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas. Cualquier punto del plano se puede localizar con respecto a un par de ejes perpendiculares dando las distancias del punto a cada uno de los ejes.
La geometría avanzó muy poco desde el final de la era griega hasta la edad media. El siguiente paso importante en esta ciencia lo dio el filósofo y matemático francés René Descartes, cuyo tratado El Discurso del Método, publicado en 1637, hizo época. Este trabajo fraguó una conexión entre la geometría y el álgebra al demostrar cómo aplicar los métodos de una disciplina en la otra. Éste es un fundamento de la geometría analítica, en la que las figuras se representan mediante expresiones algebraicas, sujeto subyacente en la mayor parte de la geometría moderna.
DISTANCIAL ENTRE DOS PUNTOS.
Las herramientas analíticas básicas son formulas para traducir los conceptos geométricos en ecuaciones y en expresiones algebraicas equivalentes.
Para determinar estas formulas, comenzaremos con el mas sencillo en la Geometría Analítica, de acuerdo con el teorema de Pitágoras.
EJEMPLO
Supongamos que tenemos estos 2 puntos en el plano cartesiano u ortogonal.
A ( 2, 4 ) y B ( 3 , 6 )
Hallar la distancia entre esos puntos:
Entonces le damos nombre a esas coordenadas.
x₁ = 2
y₁ = 4
--
x₂ = 3
y₂ = 6
Empleando la fòrmula de la distancia entre 2 puntos:
d = √ (x₂ - x₁)² + (y₂ - y₁)²
Reemplazo el valor de cada nombresito que le pusimos
d = √ (3 - 2)² + (6 - 4)²
[Realizando lo que està dentro de parèntesis]
d = √ (1)² + (2)²
[Elevamos ambos tèrminos al cuadrado]
d = √ 1 + 4
d = √ 5
La distancia es la raiz de 5
Y el resultado es : 2. 236067 ...
Y eso es todo..
Resuelto.
No hay comentarios:
Publicar un comentario